역전파(Backpropagation)

덧셈, 곱셈 역전파

덧셈, 곱셈 역전파 문제풀이(p.160)

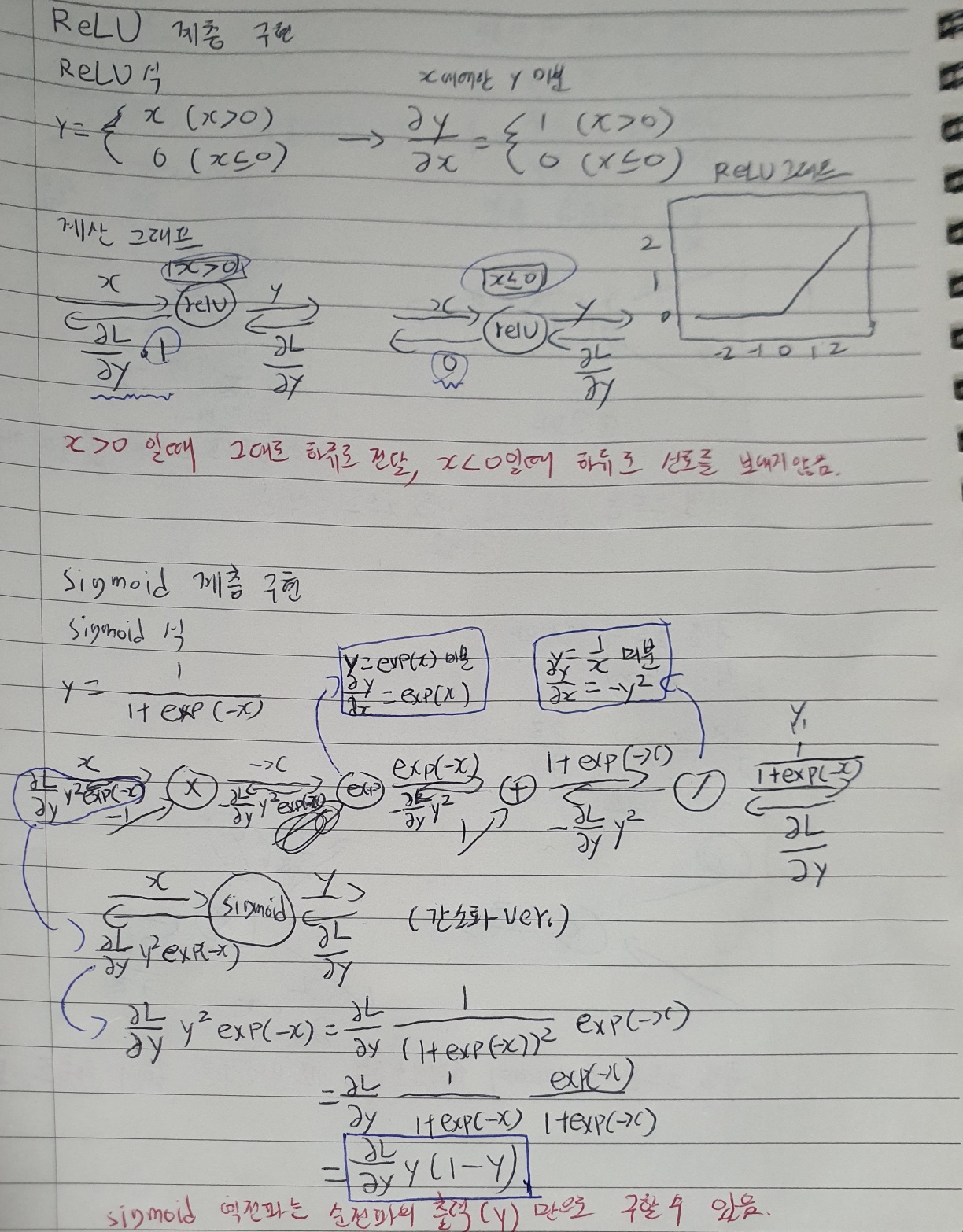
ReLU, Sigmoid 역전파

Affine 역전파

 

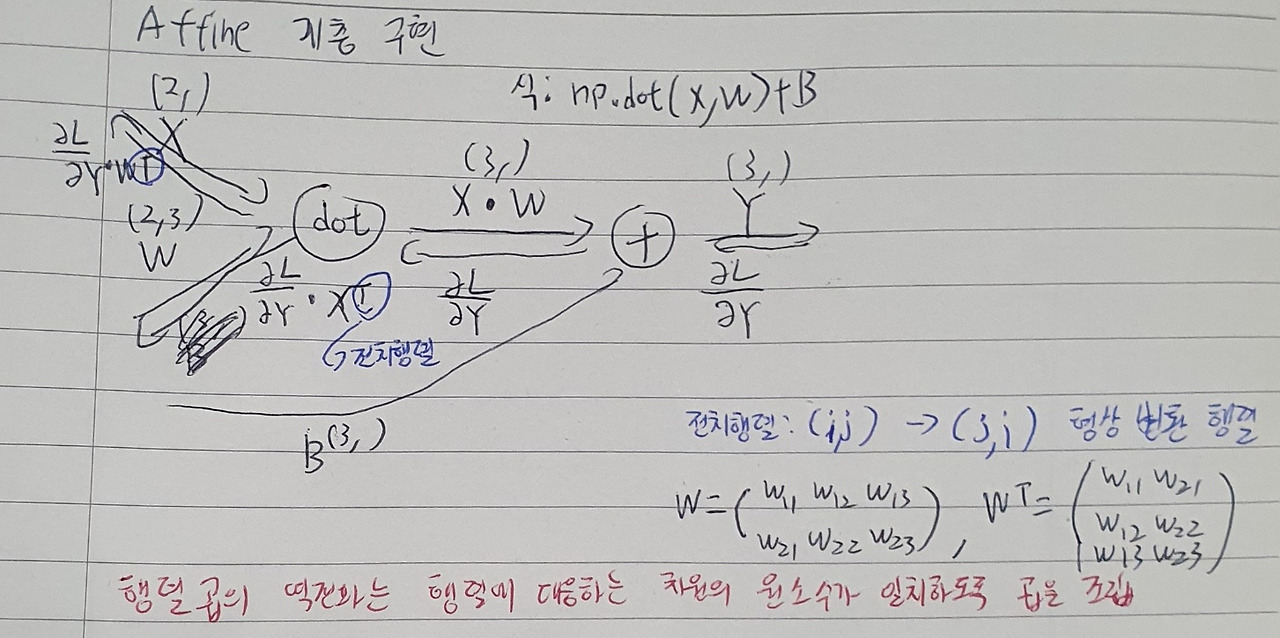
배치용 Affine 역전파

 

Softmax-with-Loss 역전파(간소화)

 

- Softmax는 입력값을 정규화(출력의 합이 1이 되도록)하여 출력한다.

- 신경망에서 수행하는 작업은 학습, 추론이 있다. 추론에서 답을 하나만 내는 경우에는 가장 높은 점수만 알면 되어서 Softmax 계층은 필요 없지만, 학습할 때는 필요하다.

- y는 Softmax 계층의 출력이고, t는 정답 레이블(One-Hot Encoding)이므로 역전파는 Softmax 계층의 출력과 정답 레이블의 차분이다. (역전파가 깔끔하게 떨어지는 이유는 Cross Entropy Error 함수가 그렇게 설계되었기 때문이다! 회귀의 출력층에서 사용되는 항등함수의 손실함수로 오차제곱합을 이용하는 이유도 같다.) 이는 Softmax의 출력에서 "index가 정답 레이블에서 값이 1인 원소"의 index 원소의 값(확률)이 낮을 때, 커다란 오차를 전파함을 의미한다.

Softmax-with-Loss계층의 계산 그래프

 

위 계산 그래프를 간소화할 시 도출되는 그래프가 간소화한 계산 그래프이다. (책의 부록 A에 도출과정이 있음)
출처 https://techblog-history-younghunjo1.tistory.com/376?category=1021615

오차역전파법 구현하기

• 신경망 학습의 순서
  
  1.  미니배치
  훈련 데이터중 일부를 무작위로 가져온다.(미니배치) 그 미니배치의 손실 함수값을 줄이는 것이 목표이다.
  2. 기울기 산출
  각 가중치 매개변수의 기울기를 구한다. 기울기는 손실 함수의 값을 가장 작게 하는 방향을 제시한다.
  3. 매개변수 갱신
  가중치 매개변수를 기울기 방향으로 아주 조금 갱신한다.
  4. 반복
  1~3단계를 반복한다.
  - 기울기 산출 단계에서 오차역전파법을 사용한다. 수치 미분으로 구현하는건 간단하지만, 계산이 오래 걸린다. 오차역전파법을 이용해 더 빠르고 효율적으로 기울기를 구할 수 있다.
  
  역전파 코드

def gradient(self, x, t):
    # forward
    self.loss(x, t)

    # backward
    dout = 1
    dout = self.lastLayer.backward(dout)
    
    layers = list(self.layers.values())
    layers.reverse()
    for layer in layers:
        dout = layer.backward(dout)

    # 결과 저장
    grads = {}
    grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
    grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db

    return grads

def backward(self, dout):
    dx = np.dot(dout, self.W.T)
    self.dW = np.dot(self.x.T, dout)
    self.db = np.sum(dout, axis=0)
    
    dx = dx.reshape(*self.original_x_shape)  # 입력 데이터 모양 변경(텐서 대응)
    return dx

 

오차역전파법으로 구한 기울기 검증
- 수치 미분의 이점은 구현하기 쉽다는 것이다. 그래서 수치 미분의 구현에는 버그가 숨어있기 어렵지만, 구현하기 복잡해 실수를 할 수 있다. 그래서 수치 미분의 결과와 오차역전파법의 결과를 비교하여 오차역전파법을 제대로 구현했는지 검증할 수 있다. 이를 기울기 확인(gradient check)라고 한다.